The basis of the magnetic refrigeration is a thermodynamic cycle that exploits the magnetocaloric effect. For practical devices, an ideal material should have a large MCE near room temperature, a low hysteresis and should contain little or no critical (rare-earth elements or cobalt) or toxic elements. The underlying design principle of high-performance magnetocaloric materials is the utilisation of a first-order magneto-structural transition – a discontinuous structural transition coupled to magnetic ordering. This leads to very large entropy changes, thus enhancing the magnetocaloric effect. Presently, the search for such materials has mostly been an intensive trial and error experimental effort. To accelerate the search for novel and optimized magnetocaloric materials, we are performing a high-throughput search for new compounds and detailed calculations of phase transitions from first principles.
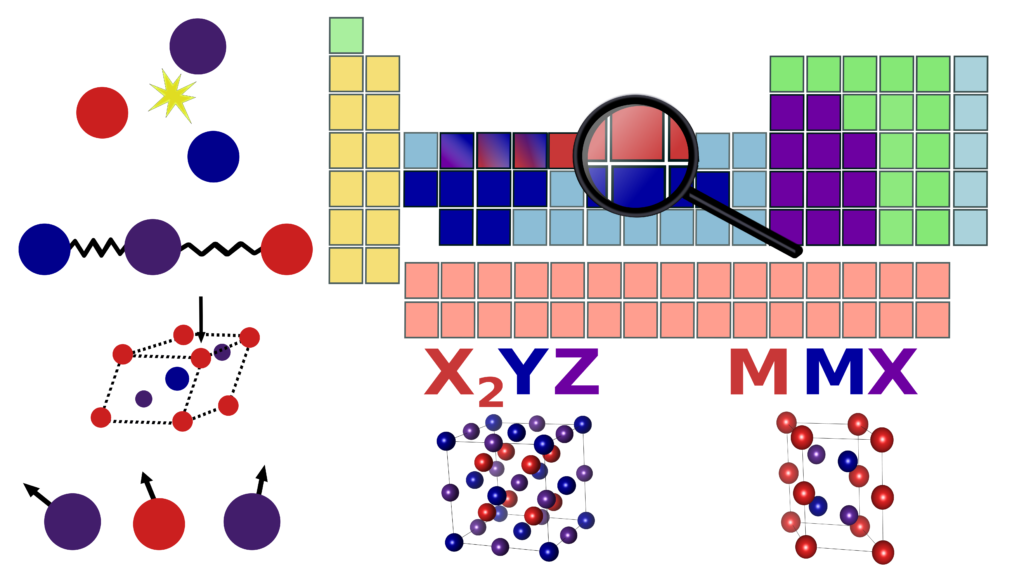
The basic concept in optimizing magnetocaloric Heusler X2YZ and hexagonal MM’X compounds is to induce strongly coupled magnetostructural transitions via substitutional disorder. We can picture this substitution as an interpolation between different isostructural compounds, to tune the magnetic and structural properties. In terms of materials discovery, we are conducting a computational high-throughput search for stable parent phases in the Heusler and MM’X classes of materials, using our in-house high-throughput environment. Next, we interpolate between these novel compounds by using the Coherent Potential Approximation within DFT to induce magnetostructural coupling and optimize magnetic properties.
The driving force behind a magneto-structural transition is a crossover of the free energy of two competing structures. At a specific temperature, the phase that is stable at lower temperatures becomes energetically unfavorable and the system transitions to the high temperature phase. To determine the stable phase at a given temperature one must minimize the free energy as a function of volume for each competing phase. The total free energy can be expressed by considering the internal energy, the vibrational and magnetic contributions, the first two can be determined by Density Functional Theory. For the magnetic term one must consider either the mean-field approximation or use Monte Carlo methods, using exchange interactions in turn obtained by DFT. By such detailed calculations it is possible to estimate transition temperatures and entropy change.



